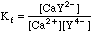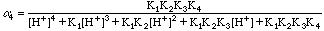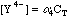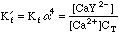Complex Formation EquationsComplex Formation Equilibrium Calculations
Conditions for EDTA Titration of Ca2+.
Goals: Compute pCa = -log[Ca2+] before the equivalence point, at the equivalence point, and after the equivalence point for the titration of Ca2+ with EDTA at the stated pH. We need a break of at least 4 pCa units for a good end point. (Rule of Four).
We will use the Initial/Final Spreadsheet method to compute each of these three points. To begin, we establish the following parameters:
The values of Alpha4 were taken from a table in the text. We could have used our spreadsheet to calculate them also, of course.
Before the End Point:
Our end point will be at 30.0 mL. Our first computed pCa value will be 10 mL before this, at 20.0 mL.
That was pretty easy. We had unreacted Ca2+, so we just computed its concentration, ignoring any contribution from the dissociation of CaY2-. pCa = -log(0.001429) = 2.85.
Now for the Equivalence point at 30.0 mL.
This will take some more work. Any Ca2+ that dissociates will free up an equal number of millimoles of EDTA, but this EDTA will dissociate into its various species, distributing as determined by the current pH. We can say, however, that
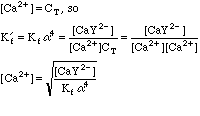
After the Equivalence Point:
Once again, this will take some work. We can't use the equations from the Equivalence Point calculation above, since we now have excess EDTA in the system, so saying that [Ca2+]=CT would be absurd. Looking back at the original equations, however, we see a simple solution for the calcium concentration.
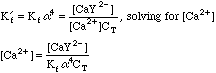 So [Ca2+] = 0.00333/(5.0E10*3.5E-01*0.00111) = 1.71E-10; pCa = 9.71
Graphing the result, we get:
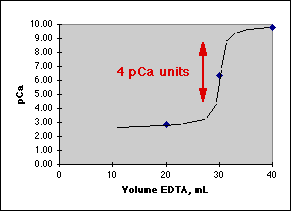 Where the Rule of Four tells us this will be a good titration.
|