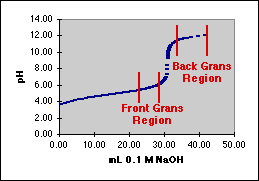
Gran's Plots for pH Titrations

Includes Error Analysis for a Least Squares Fit

©David L. Zellmer, Ph.D.
Department of Chemistry
California State University, Fresno

We wish to use Gran's Plotting for the following titration of a weak acid with a strong base using a pH meter.

Since we are doing this particular titration with a strong base, we will be titrating away the protons in the weak acid. In the Front Gran's Region we will want to plot a function that shows a linear decrease in the millimoles of H+. In the Back Gran's Region we want to plot a linear increase in the millimoles of OH-. Since our pH meter gives us pH as our readout (instead of the potentials used as an example in a previous Gran's tutorial on precipitation titrations), the equations are very simple:

Frontside Grans = (Vo+Vml)*10^(pH1front - pH)

Backside Grans = Scale Factor*(Vo+Vml)*10^(pH-pH1back)

Remember that [H+] = 10-pH. and [OH-] =10-(14-pH). By setting the pH1front term to the initial Frontside pH value, we make our first Gran's value equal to (Vo+Vml) a value that our spreadsheet will easily plot. By making pH1back equal to the last pH value we can place both graphs on the same plot. The Scale Factor removes small differences between the two, mostly for cosmetic reasons. If you wish to compute the Scale Factor, it is simply (Vo+VmlFirst)/(Vo+VmlLast).

The designations "Front" and "Back" as used above work for a strong base as the titrant. You will need to make appropriate changes when titrating with an acid. [Hint: Hydrogen ion increases as we titrate with an acid.]

Our parameter table is:

A

B
6
Vo
100
7
pH1 front
5.42
8
pH1 back
12.01
9
Scale Factor
0.87

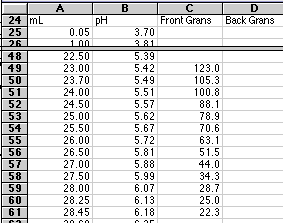
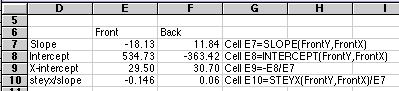
Our first Gran's Value found in cell C49 in the figure below would then be:

Cell C49 = ($B$6+A49)*10^($B$7-B49)

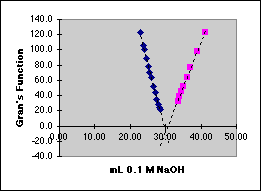
Computing the Gran's function for the two regions shown produces the following graph. The Trendline... feature of Excel 5.0 was used to draw the lines through the data.

For the statistical analysis we will use some special features of the Excel spreadsheet that depend on the Define Name... capability.

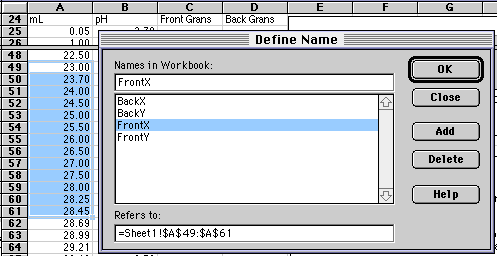
Rather than typing in $A$49:$A$61 every place we need our array of Frontside X-values, we will give this array the name FrontX. The array in column C will be given the name FrontY. To do this, drag the mouse over A49 to A61 to select it, then choose Insert/Name/Define... from the Insert Menu. (Versions of Excel other than 5.0 Mac may have Define Name... in other locations.) A dialog box will come up that will let you enter the name you want.

In the screenshot above, the array FrontX had been previously defined along with the other arrays we need. By editing the Refers to: area, we can change the numbers to which our name refers. This makes changing our statistical formulas to other data ranges easy, since the change only need be done in this dialog box. Note how these names were used in the formulas below.

Our quick and dirty estimate of the 1-sigma error for the volume intercept (steyx/slope) can be made more rigorous by using a modified form of the equation used to calculate the concentration error of a value read from a working curve. The equation given in Skoog, West and Holler, Fundamental of Analytical Chemistry, 7th Edition is:

Where (using spreadsheet formulas and the frontside arrays as examples).

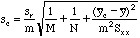
m
SLOPE(FrontY,FrontX)
sr
STEYX(FrontY,FrontX)
M
number of values for an average y-value.
N
number of data points in the line = COUNT(FrontX)
Sxx
(N-1)*STDEV(FrontX)^2
y bar sub c
the average instrument response used to compute an average y-value.
y bar
AVERAGE(FrontY)

But when our "average y-value" is the x-axis itself, y bar sub c becomes zero and the M term is removed, since y bar sub c is no longer an experimental value. The modified formula is then:

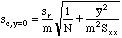
This formula is used not only for Gran's plotting, but also for standard addition methods which also use an x-axis intercept to compute the analytical result. Finally, remember that the 95%CL is tn-2sc.

The slope, m, had previously been computed in cell $E$7.

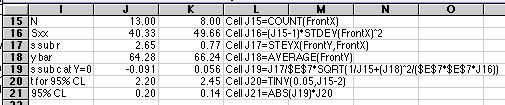
To see how our "quick and dirty" method compared with the better calculation above, compare

Front

Back
Volume intercept
29.50 mL
30.70 mL
steyx/slope (1-sigma)
0.15
0.065
2*steyx/slope (2-sigma)
0.30
0.13
s sub c at y=0
0.091
0.056
95%CL based on s sub c
0.20
0.14

The 2-sigma limits are very similar to the 95% CL, as is generally the case, so the simpler calculations based on a simple calculation of the standard deviation can be used. If you have the time and the computing power, using the full equations is still better and is more defensible in a formal report.

For the real data used in this example, our choice of Gran's regions has resulted in two volume intercepts which are significantly different from each other.

For questions or comments contact:

David L. Zellmer, Ph.D.
Department of Chemistry
California State University, Fresno
E-mail: david_zellmer@csufresno.edu

This page was last updated on 5 April 1997