A Survival Guide to Analytical Chemistry
©David L. Zellmer, Ph.D. |

What is Covered in This Guide?
- Introduction to Problem Solving
- Calculations involving Amounts.
- Calculations involving Chemical Reactions.
- Working with Concentrations.
- Putting It Together with Titration Calculations.
- Some Basic Statistical Methods.
- Solubility Equilibria.
- Acid/Base Equilibria.
- Complex Formation Equilibria
- Spectrophotometry
- Electrochemistry
Other Pages of Interest:
Introduction
There is not a lot that needs to be memorized to do analytical chemistry well. Just about everything you need to know has already been covered in the first and second semesters of Freshman Chemistry. The problem is learning to apply this knowledge to real laboratory situations. Our goal is getting you to think for yourself when faced with a laboratory problem, rather than filling in the blanks in a well-controlled laboratory exercise.
The only way you will acquire this skill is through PRACTICE. In lecture there will be assigned homework. Do this faithfully and on time. If you get stuck, ask questions during lab, during lecture, or during the office hours of your instructor. Do not wait until a day or so before an exam to start "learning" the material. In lab, learn to think through the chemistry and mathematics behind each experiment. Do required calculations yourself; don't rely on others to tell you how much to weigh out, or how to do a statistical calculation. Each step along the way is easy to learn and to do. You will only become lost if you let the material pile up on you.
The material in this Survival Guide is meant to give you a few anchor points around which you can add your own accumulated wisdom. If you don't understand the examples in this brief Guide, the more advanced material in the course will make no sense to you at all. The examples given will not cover all the things that will face you in the course, but do cover a set of basic methods that you are expected to MASTER. Your book, handouts from your instructor, and lecture notes will provide additional material. The skills required to handle all of this, however, can only come through your own efforts.
Remember, as a human being you are skilled at seeing patterns and solving problems. The lectures will emphasize the Human approach to solving problems. Even dumb (but fast!) computers can plug into a formula. Humans, however, can solve real-world problems containing poorly organized information. When faced with a complex problem in analytical chemistry:
1) Write down everything you are given about the problem. Draw pictures and arrows if necessary to make the situation clear. Include the units with any values given.
2) Clearly state what you are solving for.
3) Look at what you have written and drawn; think about how the basic operations you have learned can be used to solve this problem. It often helps to work backwards from the solution to the information you have written.
4) Identify any simpler sub-tasks that can be done first (converting grams to moles, perhaps) before solving the main body of the problem.
5) Look at the number you have generated. Does it make sense? (If you got 1.23 x 1043 M for a concentration, you have probably done something wrong!)
Calculations Involving Amounts
We use two units to describe how much of something we need to use: the gram and the mole. To these we add the prefixes of kilo-(103), milli-(10-3), micro-(10-6), and nano-(10-9). If you need to weigh something on the analytical balance, you will need the amount in grams. If you need to do a chemical calculation, the amount will almost always need to be in moles. To convert from one form to the other, just remember that
You are told to weigh out 0.40 millimoles of MgSO4 to use in an EDTA titration. The GFW (found on the label of the reagent bottle) for the solid is 120.37 grams/mole. When solving problems, always write the units down.
0.40 x 10-3 |
120.37
grams
|
Remember to check your calculation by cancelling out the units. To test yourself, convert the 0.04815 grams back into moles of magnesium sulfate.
Calculations involving chemical reactions:
First you must have a balanced chemical reaction. Precipitation, acid-base, and complex formation reactions can be balanced by inspection. Oxidation-Reduction reactions are best balanced by the half-reaction method. All calculations are done with moles. If you are given amounts in grams, convert to moles first. If you are asked for grams, do the calculation with moles, then convert back to grams at the end. The chemical reaction tells you how to convert from moles of one chemical to moles of another.
Example: How many grams of silver chromate can you get by complete precipitation of 0.1273 g of silver nitrate?
0.1273 g AgNO3
|
mole
AgNO3
|
1
mole Ag2CrO4
|
331.73
g Ag2CrO4
|
| 169.87
g AgNO3
|
2
mole AgNO3
|
mole
Ag2CrO4
|
Concentration is a property of a mixture calculated by dividing one amount by another. Commonly used concentration units include moles/liter, milligrams/liter, milligrams/kilogram, nanograms/gram, and centigrams/gram. When expressed this way, the two amounts are clearly stated. To solve for any concentration, simple figure out Amount A, figure out Amount B, then
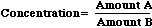
Although current practice is to express all concentrations with the defining units, it is still common to refer to concentrations by name.
Name
|
Defining
Units
|
| Molarity
(e.g. 0.1200 M)
|
moles
of solute/liter (solutions), or
millimoles/milliliter (solutions)
|
| Percent
(e.g. 23.45 %)
|
(grams
of substance/grams of sample) x 100%, or
centigrams/gram (seldom used)
|
| Parts
per million
(e.g 2.34 ppm, 2.34 mg/L)
|
milligrams/liter
(solutions), or micrograms/milliliter (solutions) milligrams/kilogram (solids), or
micrograms/gram (solids)
|
| Parts
per billion
(e.g. 0.45 ppb, 0.45 ug/L)
|
micrograms/liter
(solutions), or
nanograms/gram (solids)
|
Example 1: 25.00 mL of solution are found to contain 3.45 x 10-8 moles of fluoride ion. What is ppb F for this solution?
We need ug F/Liters to get parts per billion. First calculate "Amount A."
3.45 x 10-8 moles F
|
18.9984
grams F
|
106
micrograms
|
| mole
F
|
gram
|
Then divide by "Amount B."0.6554 ug F/0.02500 liters = 26.2 ug/L, or 26.2 ppb.
Example 2: Prepare 200 ml of 6 M ammonia solution from the 15.4 M reagent. This is often called a "dilution problem," but it can be solved from the basic definition of Molarity.
We need 200 ml of 6 M solution. We are told the volume, we need to calculate the amount of ammonia needed.
The source of the ammonia will be the 15.4 M solution. Again using the units:
1.20 moles ammonia
|
liter
of reagent
|
1000
mL
|
| 15.4
moles ammonia
|
liter
|
Add 77.9 mL of 15.4 M ammonia reagent to 100 mL of water (for safety), then dilute to 200 mL total volume.
Putting It Together with Titration Calculations
There are two calculations faced in nearly all titrations: the Standardization and the Unknown Run. In either case we have the titrant in a buret (continuous volume measuring device), and the titrate in the flask beneath it. Solution is added until an End Point is reached (usually a color change). At this point we should have added a Stoichiometrically Equivalent Amount of titrate to the titrant (see the balanced chemical equation for the reaction). The titrant in the buret is given a Concentration, usually moles/liter. The titrate in the flask is best expressed as an Amount, usually in moles.
In the examples which follow, we will use the reaction:
Example 1. We have made a solution of about 0.1 M silver nitrate titrant, but need to standardize this to four significant figures. Our standard will be solid K2CrO4. How much potassium chromate do we need to weigh out to get a titration near 30 ml?
Since this is a titration, we need potassium chromate that is "equivalent to" 30 mL of 0.1 M AgNO3. ("mmole" is "millimole" in the calculation below.)
30 mL AgNO3
|
0.1
mmole Ag+
|
1
mmole K2CrO4
|
194.20
mg
|
| mL
|
2
mmole Ag+
|
mmole
K2CrO4
|
Example 2. We weigh out 0.2774 g of potassium chromate standard. The titration takes 27.43 mL. What is the concentration of the silver nitrate titrant?
0.2774 g K2CrO4
|
mole
K2CrO4
|
2
mole AgNO3
|
|
| 194.20
g
|
1
mole K2CrO4
|
0.02743
L
|
Note how the calculations were done with either mL, mmoles, and mg; or liters, moles, and grams. Use whichever set of units seems most convenient, but remember to be consistent within a calculation.
Example 3. A solid sample weighing 0.2557 g is dissolved and titrated with the 0.1042 M Ag+ solution. We assume that all chromium in the sample was in the form of chromate ion. If 22.89 mL of titrant was required, compute % Cr in the unknown solid sample.
We know that g unknown is 0.2557 g, so our problem is half solved already. We can get g of Cr if we know moles of Cr. We can get moles of Cr if we know moles of chromate. We can get moles of chromate if we have moles of silver that reacted with it. We can get moles of silver from titration data. BINGO! The problem is solved. (This was an example of working backwards.)
22.89 mL
|
0.1042
mmoles Ag+
|
1
mmole K2CrO4
|
1
mmole Cr
|
51.996
mg Cr
|
| mL
|
2
mmole Ag+
|
1
mmole K2CrO4
|
mmole
Cr
|
Some Basic Statistical Methods.
Other handouts have a more detailed description of what you need to know. Here is a quick summary.
No measurement is perfect. When we read 22.89 mL on our burets, the measurement error is about +/- 0.02 mL. This is called an absolute error, because it has the same units as what we are measuring. Is that a lot? We answer that question by computing a relative error, perhaps in percent.
We can now compare this relative error to the relative error allowed for "good work" on a particular titration. For this titration, good work is considered to be 0.2% or less, so it looks OK. Confusion between absolute and relative error produces one of the most common mistakes on the statistics exams. If you have figured this out, you are ahead by at least five to ten points on that exam.
The total error in a analytical method is a composite of measurement errors, procedural mistakes, and imperfect chemical conversions. If the number we generate is consistently different from the "true" value, then we have poor accuracy. If we find we cannot get consistent results, then we have poor precision. The only error measurement we can usually make in lab is our precision. We do this by computing some statistics from our results. Statistics are computed by feeding our numbers into a calculator and pushing the button for either the mean (the "average value")and for the standard deviation (a measure of scatter about the mean). From the standard deviation and a t-table, we can calculate the 95% Confidence Limit (CL), a measure of precision accepted by most analytical chemists.
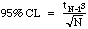
N-1
|
t
for 95%
|
| 1
|
12.7
|
| 2
|
4.30
|
| 3
|
3.18
|
| 4
|
2.78
|
| 5
|
2.57
|
The stat functions on your calculator give you a mean of 0.1055 M, and a standard deviation of 0.00375 M. The 95% CL is
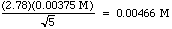
The statistics sections of most analytical books also gives you Q tests and t tests for throwing out bad data. With the small data sets we have, however, you are better off throwing out only those results you know are bad because of procedural errors. If you keep good notes in your laboratory notebook, the suspect data points will already be tagged.
Remember that your overall error in a titration will depend on the combined error from both the standardization runs and the unknown runs. To compute the overall error, first compute the relative errors for these two sets of runs, then

Example: Our standardization had a relative error of 4.42%. A similar calculation for our unknown runs gave a mean of 34.55 %Cr +/-0.14 %Cr (95% CL). To compute the total absolute error:
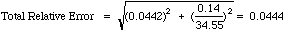
Report 34.55 +/-1.53 %Cr (More honest is 35 +/- 2 %Cr from these poor results.)
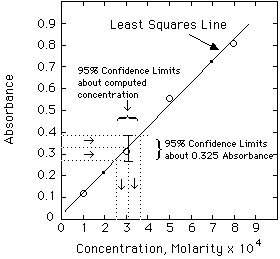
The other important statistical method is Linear Least Squares Analysis (LLS). Other handouts will tell you how to do this using a computer. The important thing to remember, however, is NOT to put a straight line through data that is not linear to begin with. Plot your data first. If is looks like a straight line, then use LLS on it.
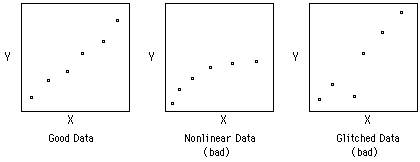
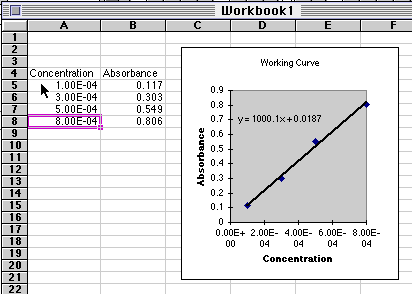
The data used in the spreadsheet program shown above are:
| Concentration
|
Absorbance
|
| 1.00
x 10-4
|
0.117
|
| 3.00
x 10-4
|
0.303
|
| 5.00
x 10-4
|
0.549
|
| 8.00
x 10-4
|
0.806
|
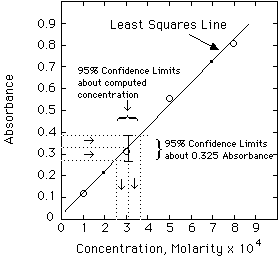
Example. The unknown has an absorbance of 0.335. Compute the concentration and estimate the error from the LLS computer results given above.
Solving the Regression Line for concentration, we get:
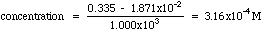
A more exact calculation of the error is possible from the LLS equations, but probably is not much of an improvement over the estimate shown above. Estimating errors from graphs seems quite mysterious to most students at first. Have your instructor lead you through a few of these until you understand it.
When you mix chemical compounds together, a precipitate may form. The solubility of this precipitate is of interest to analytical chemists because we often want 99.9+% of an ion to be converted to solid form. Only few simple mathematical relationships are needed to do these calculations.
Consider:
Type 1: Either Ag+ or CrO2-4 are in excess (usually called a Common Ion problem). This is the situation most often encountered, and the easiest to solve.
Example 1: After precipitation of silver nitrate with potassium chromate, the excess chromate is 0.012 M. Calculate the concentration of [Ag+] in solution.
Solving Ksp for [Ag+], we get
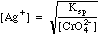
Plugging in we get
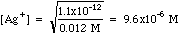
For other compounds the Ksp may have a different form, but solving for the ion you need is a simple exercise in algebra.
Type 2: If there is no excess silver or chromate, then we have a more complicated situation mathematically. We somewhat misleadingly call this case Simple Solubility.
Example 2: What is the concentration of silver ion if solid silver chromate is allowed to equilibrate with pure water?
Charge Balance tells us that since silver and chromate are the only ions in solution , (Contrast this with Example 1, where a [K+] term and a [NO3-] would have to be added because of the excess potassium chromate added to the silver nitrate.)
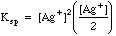
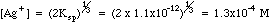
Many students make the mistake of using the methods of example 2 for all solubility problems, whether there is excess ion present or not. The way to tell which ions may be present in excess after a reaction has taken place is to do some simple bookkeeping. The example below shows the Initial/Final Spreadsheet Method for following the amounts in chemical reactions.
Example 3: 25.0 mL of 0.10 M AgNO3 is mixed with 36.5 mL of 0.15 M K2Cr04. What is the concentration of silver ion after reaction?
Ag+
mmoles
|
NO3-
mmoles
|
K+
mmoles
|
CrO42-
mmoles
|
Ag2CrO4(s)
mmoles
|
Volume
mL
| |
| Initial
|
2.50
|
2.50
|
10.95
|
5.475
|
0
|
25+36.5
|
| Final
|
0
|
2.50
|
10.95
|
4.225
|
1.25
|
61.5
mL
|
| Molarity
|
0.0687M
|
Work through how these numbers were determined. The Initial millimoles are simply the milliliters (mL) of each solution times the molarities (millimoles/mL). For K+, there are two potassium ions for each chromate. The Final millimoles are calculated from the chemical reaction between silver and chromate. Remember that two silver ions react with one chromate ion. Nitrate and potassium are Spectator Ions; their millimoles do not change. Silver is (almost) all wiped out, with chromate left in excess. We are left with a Common Ion problem. The chromate concentration is obtained by dividing the millimoles of chromate (4.225 mmoles) by the milliliters of solution (61.5 mL). Plugging this into Ksp as done in example (1) above, we get:
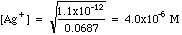
This may seem pretty complicated, but is just an example of writing everything down that we know, then solving for what we need. Each step is simple. Looking at the information and organizing it into a solution takes thought and practice. It cannot be learned the night before an exam.
More advanced solubility product problems build on these basic ideas. For example, the concentration of excess chromate calculated in Example 3 is not really the Equilibrium Concentration [CrO42-] needed in the Ksp expression, but is actually the Analytical Concentration Cchromate = (mmoles excess chromate/mL of solution), and will be slightly smaller than the equilibrium concentration. In this example the difference is too small to matter, but in cases where the solubility of the precipitate is fairly high, more advanced methods will be needed based on the use of all the terms in the charge balance expression. The Initial/Final spreadsheet will help in the calculation of many of these terms.
We have also neglected the effect of ionic strength on the activity of the ions, resulting in an apparent increase in the value of the Ksp. Ionic strength and activity calculations begin with an Initial/Final spreadsheet to catalog all the ions present.
There are five monoprotic acid/base systems (and one polyprotic) you must be able to solve without fail:
Type
|
Examples
|
Approximate
Formulas
|
| Strong
Acid
|
HCl,
HNO3, H2SO4 (first proton), HClO4
|
[H+]
= CSA, (if CSA > 10-6)
pH = -log [H+]
|
| Strong
Base
|
NaOH,
KOH, Ba(OH)2
|
[OH-]
= CSB, (if CSB > 10-6)
[H+] = Kw/[OH-]
|
| Weak
Acid
|
Acids
with a Ka, e.g. CH3COOH, or salts of weak bases, e.g.
NH4Cl.
|
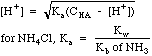
|
| Weak
Base
|
Bases
with a Kb (mostly amines, e.g. NH3), or salts of weak
acids, e.g. CH3COO-Na+.
|
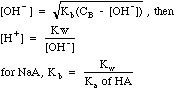
|
| Buffer
|
Mixtures
of weak acids and their conjugate bases, e.g. CH3COOH mixed with
CH3COO-Na+
|
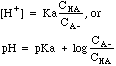
|
| Amphoteric
(polyprotic)
|
NaHCO3,
KHPhthalate
|
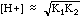
|
Strong acids and bases ionize completely, so there is no equilibrium expression. Only the dissociation of water H20 = H+ + OH- , Kw = [H+][OH-] = 10-14, sometimes expressed as pH = 14 -pOH, needs to be used on occasion to convert between pH and pOH.
Weak acids ionize only partially, and have an equilibrium expression
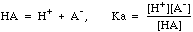
Note the distinction between CHA, the molar concentration of the weak acid we think we have placed in the system, and [HA], the equilibrium concentration that actually exists in solution.
Weak bases hydrolyze in water, which seems like something different from weak acids. The equations produced are almost identical, however, if you swap H+ and OH- as well as Ka and Kb. To confuse students further, the Kb that describes the hydrolysis of a salt of a weak acid is called a Kh in most textbooks. Here Kh and Kb are just called Kb.

The biggest problem students seem to have is recognizing what kind of acid/base system they are solving for. The list of common strong acids and bases is very short and is given in the table above. Memorize these. Almost everything else will be weak. Buffers are recognized by the presence of both the conjugate acid and the conjugate base of a weak acid or base. In simple problems you will be told what the substances are. In more complicated problems you will be given some chemical that react. It that case you need to use the Initial/Final Spreadsheet Method to determine what is in solution after the reaction is over. Then choose the appropriate acid/base system and solve the equations.
The formulas given above are approximate, but work in so many cases that you would probably be forgiven for misapplying these on occasion. More advanced students will be able to derive these from mass balance, charge balance and the equilibrium expressions, and will know the limitations of the formulas used. Lecture will cover a host of applications not covered here, such as acid/base titration curves and fraction-of-species calculations.
Example 1. What is the pH of 0.0020 M NaOH?
This is a Strong Base. [OH-] = 0.0020 M.
pOH = -log (0.0020) = 2.70. pH = 14 - 2.70 = 11.30
Example 2. What is the pH of 0.045 M benzoic acid?
This is not one of the strong acids listed, so it is probably a weak acid. In the back of our analytical book we find that Ka = 6.3 x 10-5. Plugging into the formula:
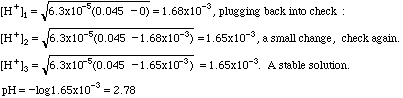
If you cannot get a stable solution by this means, you must convert this expression into a quadratic equation and solve it by the method you learned in algebra.
Example 3. 3.45 millimoles of acetic acid are mixed with 2.14 millimoles of sodium acetate in 100 mL of distilled water. What is the pH of the solution?
Acetic acid and sodium acetate form a conjugate acid/base pair. That makes this a buffer problem. A look in the back of the book gives us Ka = 1.75 x 10-5. pKa = -log(1.75x10-5) = 4.76.
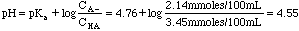
Example 4. 21.3 mL of 0.10 M NH3 is mixed with 15.6 mL of 0.10 M HCl. What is the pH of the resulting solution?
NH3 is a weak base. HCl is a strong acid. This mixture seems not to fit into any of the categories above. But wait! Acids and bases REACT with each other (unless they are conjugate acid/base pairs). This calls for an Initial/Final Spreadsheet.
H+
mmoles
|
Cl-
mmoles
|
NH3
mmoles
|
NH4+
mmoles
|
Volume
mL
| |
| Initial
|
1.56
|
1.56
|
2.13
|
0
|
21.3
+ 15.6
|
| Final
|
0
|
1.56
|
0.57
|
1.56
|
36.9
mL
|
| Molarity
|
0.0154M
|
0.0423M
|
We again ignore the spectator ions. What is left is a BUFFER. The Kb of NH3 is 1.75 x 10-5. pKb = -log(1.75x10-5) = 4.76; pKa = 14 -pKb = 9.24.
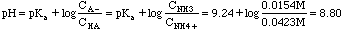
Example 5. In lab we are asked to do a titration curve for potassium hydrogen phthalate. 3.00 millimoles of KHP are dissolved in 50 ml. What is the beginning pH of this titration?
KHP (P stands for phthalate here) is an amphoteric substance. (HP- could accept a proton and act like a base; on the other hand it could give up its proton and act like an acid. This substance does not fall into any of our first five categories.). The parent polyprotic acid is o-phthalic acid. The back of the book gives us K1 = 1.2x10-3, K2 = 3.9x10-6.
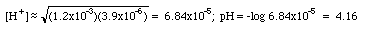
This equation is an approximation. Your textbook will have the longer and more accurate expression.
Complexing agents are used to bind certain classes of metal ions, forming soluble complex ions. An important complexing agent used for titrations is EDTA, called Y4- for short. The equilibrium constant for the formation of the complex ion is called (surprise!) the Formation Constant, Kf. Metals like calcium--which have very little interesting chemistry--will form complexes with EDTA that can be used for titrations.
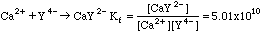
Example 1. 45.3 ml of 0.0100 M EDTA is added to 0.300 millimoles of Ca2+ dissolved in 50.0 mL of distilled water. What is the concentration of Ca2+ if all of the excess EDTA is present as Y4-?
This calls for the Initial/Final Spreadsheet once again. (In the next example we will add a modification that deals with EDTA that is not all present as Y4- due to pH effects, so stay tuned.)
Ca2+
mmoles
|
Y4-
mmoles
|
CaY2-
mmoles
|
Volume
mL
| |
| Initial
|
0.300
|
0.453
|
0
|
50
+45.3
|
| Final
|
0
|
0.153
|
0.300
|
95.3
mL
|
| Molarity
|
0.00161M
|
0.00315M
|
Solving Kf for Ca2+ we get
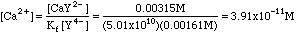
That was easy enough, but it was not entirely accurate, as the next example will show.
EDTA is a polyprotic acid as well as a complexing agent. This means it can exist as a combination of the species H4Y, H3Y-, H2Y2-, HY3-, and Y4-. There will be four acid equilibrium constants, K1, K2, K3, and K4. The fraction of the species that will be the Y4- we need can be calculated from these equilibrium constants and the mass balance relationship:
Where CT is the total concentration of all free EDTA species in solution. In Example 1 above, CT would be 0.00161M. To calculate the true concentration of Y4-, we need the fraction of species a4, where
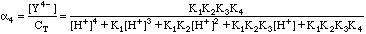
Although messy, calculating a4 at any given pH is straightforward. We can now calculate the true value for [Y4-]. It is
Example 2. Calculate the concentration of Ca2+ from example 1 at pH = 10 and at pH = 6.
At pH 10, a4 = 3.5x10-1; at pH 6, a4 = 2.2x10-5.
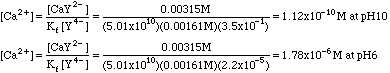
Most simple calculations done for spectrophotometry involve reading concentrations from working curves followed by dilution calculations. (See the Linear Least Squares example in the Statistics sections above.) Metals are often measured by determining the absorbance of a colored complex, so we need to be sure the complexation is complete by controlling the pH and concentration of the complexing agent. The only other things that need to be calculated involve Transmittance and Absorbance.
To do spectrophotometry in the laboratory we must be familiar with the components of a spectrophotometer. These are the light source (will it emit at the wavelength needed?), the monochromator (will it provide good resolution with low stray light?), the sample cell (will it transmit the wavelength selected?), the detector (will it detect the wavelength selected?), and the readout electronics (should we read out in absorbance, transmittance, or something else?).
We shine a band of colored light of power P0 through a cell; it comes out with power P. Transmittance is simply
Absorbance and Transmittance can be calculated from each other by:
Absorbance is related to concentration through the absorptivity "a", the cell path length "b" (usually in centimeters), and the Concentration "C". The relationship is called Beer's Law and is simply
If C is in moles/liter, then "a" is called the molar absorptivity with units of cm-1mole-1liters and is often given the symbol [epsilon]. If other concentration units are used, then "a" has whatever units it takes to make Absorbance come out dimensionless.
The optimum absorptivity is obtained by running a spectrum of our compound. This plot of absorbance vs. wavelength is used to find a peak of maximum absorbance that is not near peaks of interfering substances.
To do a spectrophotometric analysis we measure the absorbance of a series of standard solutions, then plot A vs. C. If Beer's Law is obeyed, we will get a straight line that can be used to measure the concentrations of unknown solutions.
Example: An iron-phenanthroline complex has a concentration of 10.0 ug Fe/mL and gives a %T of 1.3% in a 1.00 cm cell at 520 nm wavelength using an inexpensive Spectronic 20 spectrophotometer. Calculate the absorbance and the absorptivity of this complex, then state if this is a good standard solution to use.
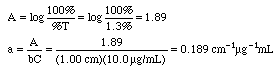
A Spectronic 20 would not give good measurements at 1.89 A, since that is well above 1.0 A. Either lower the concentrations to around
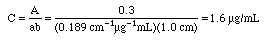
or use a more expensive spectrophotometer that can measure above absorbance 1.0. At this high absorbance Beer's Law would probably not be followed on an inexpensive Spectronic 20, so any calculations using it will contain a lot of error. The calculation shown can be used to estimate a better concentration to try next, however.
Oxidation/Reduction reactions proceed by the transfer of electrons from a donor of electrons to an acceptor. The charge transfer reactions, the identities of the donors and acceptors, and the relative energies involved are summarized in the table of Standard Reduction Potentials found in the backs of most analytical chemistry books. Two examples are:
| Cr2O72-+ 14 H+ + 6e- = 2Cr3+ + 7H2O | Eo = 1.33 volts
|
| Fe3+ + e- = Fe2+ | Eo = 0.771 volts
|
Which can be used as a titration reaction for the determination of Fe2+ by dichromate. Using more conventional terms, Cr2O72- is called an oxidizing agent, and Fe2+ a reducing agent.
It is possible to measure the potential energy difference in these half-reactions directly. Assume we set up the following electrochemical cell
in which "|" stands for the phase boundary between the Pt electrode and the contents of the cell, and "||" stands for a salt bridge between the left hand side of our cell and the right side which contains a reference electrode. Next attach an electrometer between the Pt of the left side and the electrode of the SHE on the right. The potential we would measure is
The SHE is a reference electrode defined as having a potential of 0.000 volts. Emeas then depends on the E value of the dichromate/Cr3+ half reaction. We compute this potential from the Nernst Equation
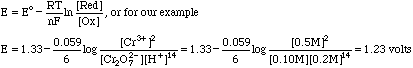
Our measured potential is then
Many analytical texts go on to confuse the student with talk of anodes (electrodes where oxidation occurs) and cathodes (electrodes where reduction occurs). In our example above, electrons would be attracted to the positive Pt electrode where they can cause reduction, so it would be the cathode. The SHE is the anode.
Applications of electrochemical calculations occur in redox titration curves, and in potentiometry. In potentiometry, we measure a potential and use it to calculate a concentration directly. pH electrodes are a good example of this.
S and K are determined by calibration against known H+ standards. From then on, a measurement of E will give us pH =(E - K)/-S.
A redox titration curve of Emeas vs mL of titrant can be calculated by using an Initial/Final Spreadsheet to determine solution composition after a known addition of titrant. The appropriate Nernst Equation is used to calculate the potential.
Example: 50.0 mL of solution containing 3.00 millimoles of Fe2+ is titrated with 23.5 mL of 0.01667M Cr2O72- . Compute the potential of the resulting solution against an SCE reference electrode of 0.242 volts. The H+ concentration may be assumed to be constant at 1.0 M.
| Cr2O72-
mmoles
|
Cr3+
mmoles
|
Fe2+
mmoles
|
Fe3+
mmoles
|
Volume
mL
| |
| Initial
|
0.392
|
0
|
3.00
|
0
|
23.5+50
|
| Final
|
0
|
0.784
|
0.650
|
2.350
|
73.5
mL
|
| Molarity
|
0.0107M
|
0.00884M
|
0.0320M
|
The only half reaction with non-zero values is that for Fe3+/Fe2+, so we use that Nernst Equation
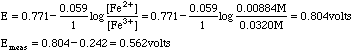
The only place this method does not work well is at the equivalence point of the titration. Here we need to take a weighted mean of the potentials.
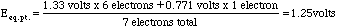
Conclusion
Remember that the examples in this brief Guide do not include everything you will learn in your Analytical Chemistry class. Many more applications will be covered in lecture and in laboratory. Experience has shown, however, that students who do not learn the fundamentals presented here, generally are not able to understand the additional material presented. So make sure you understand these examples well. They will help you survive the rest of the course.