Spreadsheet Equivalents of Least Squares Formulas
©David L. Zellmer, Ph.D.
Department of Chemistry
California State University, Fresno
May 9, 1997
Spreadsheet Equivalents of Least Squares Formulas
©David L. Zellmer, Ph.D. |
It seems that every textbook that shows chemists how to perform some basic statistical analyses chooses to define the quantities differently and uses different terminology. Some newer additions have started to incorporate computers into the statistical analyses, but this is often reduced to having students use a spreadsheet to compute sums of squares which are then used in traditional calculations. While there may be some pedagogical value to this, hard working chemists would rather cut to the chase and get the calculation done.
This guide shows how the equations in the following books are translated into their spreadsheet equivalents using Microsoft Excel. (Macintosh version number 5.0. Formulas for the equivalent PC version of Excel are the same.)
CDM was a Dover release of an old Navy training manual in statistics, and must now be out of print. It was the first book I had found that covered the basic statistical methods I wanted to use in chemistry and gave clear examples. For linear least squares analysis it emphasizes computing the uncertainties of using a least squares line to predict new values of Y, assuming that the X-values are very accurately known. Many of the statistical handouts that I have provided over the years have been based on this book. The equations from this book are provided for those who wish to "computerize" this older material using Microsoft Excel.
SWH reflects more recent publications that show how to compute the uncertainties when linear least squares analysis is applied to typical analytical chemistry working curves. When preparing a working curve, we prepare N accurately known standards (X=concentration), then measure the instrument response (Y=response) for each. Instead of using the least squares line to have X predict a new value of Y as CDM would do, the analytical chemist wishes to use M measurements of the response of the instrument to an unknown, then compute X (concentration) with its associated uncertainty. Using an error prone Y measurement to predict X involves more error than using an accurate X to predict Y from the least squares line. The "1/M" term in the SWH equation for "s sub c" provides this additional error.SWH follows the "generic" approach to least squares analysis, using equations that do not require any special statistical functions for their calculation. While admirable, this results in very bulky calculations on computer spreadsheets. The equations below make use of the functions built into Microsoft Excel, version 5.0, to streamline the calculation process.
It has been my experience that students using fairly complicated equations to compute errors often make trivial mistakes in setting up the equations. To aid them in recognizing poor calculations, I urge them to (1) look at the data -- does the computed scatter make sense given the observed scatter of the data, and (2) use a "quick and dirty" error estimate such as "2 sigma" where the confidence limit for a computed X is often near 2*STEYX()/SLOPE(), where STEYX() and SLOPE() are statistical functions that can be computed in one step using Microsoft Excel.
For the equation of a straight line:
Equation in Algebraic Form
(most are from Crow, Davis, and Maxfield, Statistics Manual, Dover 1960)
|
Spreadsheet
(Microsoft Excel 5.0)
|
| N
= number of x,y data points.
|
=COUNT(X-array), or use Y-array.
|
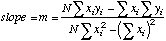
|
=SLOPE(Y-array,X-array)
|
|
=INTERCEPT(Y-array,X-array)
Note that slope and intercept, plus other LLS statistics can also be calculated
from =LINEST(Y-array,X-array [,parameters]).
|
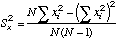
|
=STDEV(X-array)^2
|
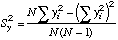
|
=STDEV(Y-array)^2, but we won't need this.
|
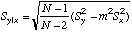
|
=STEYX(Y-array,X-array)
|
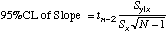
|
Compute
from previous values, but note that instead of using a table, t can be
calculated from =TINV(Probability,degrees of freedom)
e.g. =TINV(0.05,COUNT(X-array)-2)
|
| The
95% C.L. of a y value given an X value, computed from y'=mX+b. (this is called a regression value, or y')
If you set X=0, you get the 95%CL of the Intercept.
|
Compute
from previous values, but note that
This calculation may underestimate the error because we assume a "perfectly" known value of X when computing Y. See the corresponding equation from SWH below.
|
| When
using a working curve, such as Absorbance vs. Concentration, we often specify y
(Absorbance) and compute X (Concentration). If you plug this X into the
equation above and compute the 95% C.L. of y', then
|
Compute from previous values.
Because uncertainties in measuring Y are not included, this equation will underestimate the error in X. See the equation for "s sub c" in the SWH section below
.
|
| Equations
from Skoog, West, and Holler, Fundamentals of Analytical Chemistry, 7th
Edition, Saunders 1996
|
|
| SWH
starts with the premise that you will first calculate several sums of squares
from the X,Y data, then use these values to calculate the LLS statistics. This
could be a good approach if your spreadsheet lacks advanced statistical
functions.
|
The
"plain vanilla" way requires that you set up five columns: X, Y, X*X, Y*Y,X*Y.
The first two colunns hold your X,Y data. The last three columns are computed
from the first two.
are computed by summing each of the five columns. Sxx, Syy, and Sxy are calculated from these sums.
In the spaces below I will show more advanced alternatives to this.
|
| A
note to the Statistically Savvy: This "S" looks like a variance, but it is
not. It is just the sums of squares of the deviations of X from the mean X.
|
N=cell
reference to where N is.
=(N-1)*STDEV(X-array)^2, or
=N*VARP(X-array), a Variance formula.
|
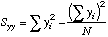
|
=(N-1)*STDEV(Y-array)^2, or
=N*VARP(Y-array), a Variance formula.
|
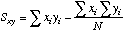
|
You
could compute this using the values computed from the "plain vanilla" way
described above, or you could use:
=SLOPE(Y-array,X-array)*(cell ref to Sxx)
|

| =AVERAGE(X-array), and
=AVERAGE(Y-array)
|
Slope
of the line
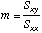
|
=SLOPE(Y-array,X-array)
|
Intercept
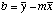
|
=INTERCEPT(Y-array,X-array)
|
| Standard
Deviation about regression;
|
=STEYX(Y-array,X-array)
|
| Standard
Deviation of the slope:
|
Compute from previous values.
|
| Standard
Deviation of the intercept:
|
See the calculation of the CL of the intercept in the first section above.
|
| Standard
Deviation of an X-value read from a calibration curve. "s sub c"
|
This can be computed from previous values. You will find that the errors computed here are larger than in the CDM equations given above because of the additional uncertainty of the Y measurement that intersects with the regression line to produce a corresponding X-value. The 1/M term provides the additional error in X.
|
| 95%CL
= tn-2sc
|
=TINV(0.05,(cell
ref to N)-2)*(cell ref to sc)
|
|
The following equation does not appear in SWH, but is easily derived from "s sub c." Standard Deviation of the X-axis intercept. This is used in Gran's Plots and in Standard Addition Plots when the X-axis intercept provides the computed value.
|
This can be computed from previous values.
The 1/M term vanishes, since the X-axis is assumed to be a "perfectly known" Y value. |
David L. Zellmer, Ph.D.
Department of Chemistry
California State University, Fresno
E-mail: david_zellmer@csufresno.edu
This page was last updated on 9 May 1997