The Math Major Vol. 3, No. 11
The Math Major
CSU Fresno Mathematics Department
Vol 3. No. 11 (March 22, 1999)
Editor: Dr. Larry Cusick.
Colloquium
- Date: Thursday March 25, 2:10
- Location: Science 143
- Speaker: Dr. Don Chakerian, UC Davis
- Title: "Some Elementary Properties of Ellipses"
- Description: Dr. Chakerian will speak on some elementary properties of ellipses
that are not well know and perhaps deserve wider publicity.
Putnam Results
The Fifty-Ninth Annual William Lowell Putnam Mathematical Competition was held in December
1998. There were a total of 2581 contestants representing 419 colleges and universities in Canada
and the United States. The seven CSU Fresno contestants were Anar Ahmedov, Mike Chamberlin,
Arkady Hanjeiv, Leslie Hatcher, Shawn Jackson, Alice Klepac and Matthew Zhou. The math
department would like to express its sincere appreciation to these seven students for accepting
the Putnam challenge. The top scoring Fresno contestant was Alice Klepac. Alice will receive a
$100 first place award. The second highest Fresno score was Anar Ahmedov. Anar will
receive a
$75 second place award.
Math Awareness Month \& the Field Day
The Joint Policy Board for Mathematics, comprised
of three national mathematics societies--the Mathematical Association of America, the American
Mathematical Society, and the Society for Industrial and Applied Mathematics--has announced that
the theme for April 1999's annual Mathematics Awareness Month will be "Mathematics and Biology."
The theme will highlight the importance of mathematics as an essential element of scientific
advancement in biological research, including blood flow modeling, brain research, the human
genome project, epidemiology, research analysis and other bio-technical fields.
As part of the Mathematics Awareness Month events, our math department will host its annual
Mathematics Field Day on Saturday April 17. Field day events include mathematics competitions
for area high school students.
A Mathematical Quote
"The traditional mathematics professor of the popular legend is absentminded.
He usually appears in public with a lost umbrella in each hand. He prefers
to face the blackboard and to turn his back to the class. He writes a, he
says b, he means c; but it should be d. Some of his sayings are handed down
from generation to generation.
`In order to solve this differential equation you look at it till a solution
occurs to you.'
`This principle is so perfectly general that no particular application of it
is possible.'
`Geometry is the science of correct reasoning on incorrect figures.'
`My method to overcome a difficulty is to go round it.'
`What is the difference between method and device? A method is a device
which you used twice.'
--George Polya (1887-1985)
 George Polya
George Polya
Problem Corner
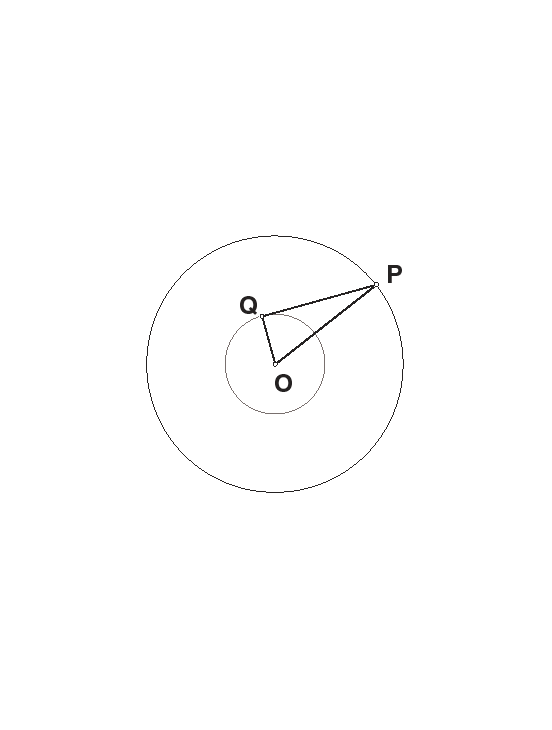
Problem 3.10: Let C be a circle with center O and Q a
point inside C different from O. Where should the point P be located on the circumference
of C to maximize the measure of angle OPQ?
Solution to Problem 3.10: Think of P as fixed, while Q varies along the circle about O
with radius OQ. It is then clear that angle OPQ is maximum when PQ is tangent to the small
circle, that is, when angle OQP = 90 degrees.
Correct solutions were received from John Jamison and Jon Klassen.
New Problem
Problem 3.10: (Due Thursday April 8, 3 p.m.) Let k be a positive integer. Find the largest
power of 3 which divides 10k - 1.
Solutions may be delivered to the
math department office (for Dr. Cusick) or by e-mail.
CSU Fresno Math Department Home
Page
California State University, Fresno


