Math 100. Exploring Mathematics. Spring 2009.
Problems.
1. (Cookie Jar Problem) There was a jar of cookies on the table. Amanda was hungry because she hadn't had breakfast, so she ate half the cookies. Then Beth came along and noticed the cookies. She thought they looked good, so she ate a third of what was left in the jar. Christine came by and decided to take a fourth of the remaining cookies with her to her next class. Then Daniel came dashing up and took a cookie to munch on. When Eva looked into the cookie jar, she saw that there were two cookies left. "How many cookies were there in the jar to begin with?" she asked.
2. (Tile Problem) An artist is planning to construct a rectangular wall design from square tiles. The wall is 72 inches long and 42 inches wide. All the square tiles must be the same size, and the length of the sides must be a whole number of tiles.
3. (Boxes) A carpenter has three large boxes. Inside each box are two medium-sized boxes. Inside each medium-sized box are five small boxes. How many boxes are there altogether?
4. (Pick the Numbers) Given seven numbers 2, 3, 4, 5, 7, 10, 11, pick five of them that when multiplied together give 2310. Find as many different solutions as you can.
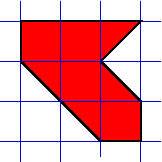
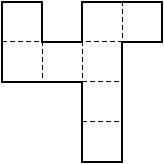
5. (Find the Area) Find the area of the figure shown below. Which of the problem strategies have you used? Find at least two (or more: as many as you can) different solutions.

6. (Geoboard) Create other shapes (similar to 5) using Geoboard and find their areas. Use as many different problem solving strategies as possible.
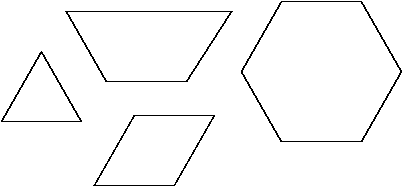
11. If the area of the triangle is 1 square unit, what are the areas of the other three figures?
12. If the area of the hexagon is 1 square unit, what are the areas of the other three figures?
13. If the side of the triangle is 1 unit, what are the areas of all four figures?
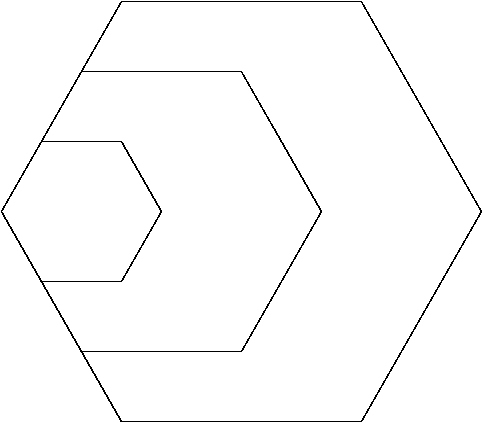
14. If the area of the given hexagon is 1 square unit, what is the area of the hexagon whose each side is twice longer? What if each side is three times longer? Cover such hexagons with the above figures and verify.
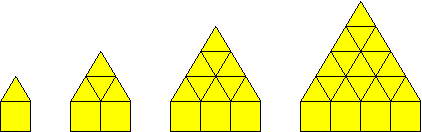
21. For each of the following sequences of figures:
(a)

| Figure in sequence | Number of squares | Area | Perimeter |
| 1st | 4 | 4 square units | 10 units |
| 2nd | |||
| 3rd | |||
| 4th | |||
| 5th | |||
| 50th |
(b)

(c)
22. Create your own sequence of figures (using rectangles, triangles, hexagons, or any other shapes you like). Find the number(s) of shapes needed for the 50th figure in your sequence. Can you also find its area and/or perimeter?
23. Find the following sums:
24. Calculate the following the differences:
25. Calculate the following sums (reduce your answers):
26. The sequence 1, 1, 2, 3, 5, 8, 13, ... , where each number is equal to the sum of two previous numbers, is called the Fibonacci sequence. The numbers in this sequence are called Fibonacci numbers.
27. Calculate the following sums:
|
|
31. Write and solve your own story problems involving fraction addition and subtraction (one problem for each operation, so you need two separate problems) similar to those in the article you've read.
32. Write and solve your own story problems involving fraction multiplication and division (one problem for each operation, so you need two separate problems) similar to those in the article you've read.
33. Two-thirds of a fish weighs 10 1/2 pounds. How heavy is the whole fish?
34. A suit is on sale for $180. What was the original price of the suit if the discount was 1/4 of the original price? Explain how you found your answer and how you can check your answer.
35. James uses 1 1/2 cups of milk and 2 1/4 cups of flour for his favorite cookie recipe. This makes 60 cookies. How much milk and flour would he need to make 40 cookies?
41. The figure shown consists of 8 congruent squares. The perimeter of the figure is 36 units. What is the area of the figure?
42. The cafeteria sells each apple at one price and each banana at another price. For 1 apple and 3 bananas Jose pays $2.05. For 4 apples and 2 bananas April pays $2.70. Maria buys 2 apples and 2 bananas. How much does she have to pay?
43. There are 8-legged spiders and 6-legged flies in a room. The total number of insects is 80. The total number of insect legs is 604. How many more spiders than flies are in the room?
44. A tractor has 14 gallon gasoline tank. The tractor starts with a full tank of gasoline. It runs out of gasoline when it is done plowing 3/5 of a field. How much gallons of gasoline does the tractor need to plow the whole field?
45. If the length of a rectangle is reduced by 50% and the width of the rectangle is increased by 50%, how does the area of the rectangle change?
46. An animal walks 30 feet in 5 seconds. What is the speed of this animal in miles per hour?
51. Use the base 10 manipulatives to calculate:
52. Represent the following problems on a number line.
53. Place the digits 1, 2, 3, 6, 7, and 8 in the boxes below to obtain
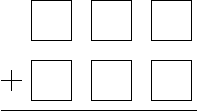
(a) the greatest possible sum;
(b) the smallest possible sum.
Explain your strategy!
54.
A group of second grade students are playing the following game.
They write digits from 1 to 9 in a row, and put a "+" or a "-" between every two consecutive digits. Then they calculate the result. For example,
1+2+3-4+5+6-7+8-9=5,
1+2-3+4+5-6+7+8-9=9, etc.
The goal is to come up with a sequence of +/- signs for each answer between 1 and 10. (The person who first comes up with 10 sequences, one for each answer, will
win.) Is it actually possible to do this?
55. Modify the game in problem 54 as follows: allow any order of the 9 digits, e.g. 4+8-1+5-7+3+6-2-9. Will your answer to the question in problem 54 change?
56. What if in the game in problem 54 we allow "combining" two or more consecutive digits, to form two- or more digit numbers. E.g., 123-4-56-7+8-9 will now be allowed. Will your answer to the question in problem 54 change?
57. Read the following article: Understanding Subtraction (part of section 3.1 from "Mathematics for Elementary School Teachers" by T. Bassarear, a link is available on the course schedule page). Answer the following question: Do you agree that "trading" (or "renaming" or "regrouping") is a better term than "carrying" or "borrowing"? Why or why not? If so, which term do you like most and why?
58. Place the digits 1, 2, 3, 6, 7, 8 in the boxes shown below to obtain
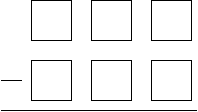
(a) the greatest possible difference;
(b) the smallest possible positive difference.
Explain your strategy!
59. A mule and a horse were carrying some bales of cloth. The mule said to the horse, "If you give me one of your bales, I shall carry as many as you." "If you give me one of yours," replied the horse, "I will be carrying twice as many as you." How many bales was each animal carrying? Find as many different solutions as you can.
61. Using divisibility tests by 2, 3, 4, 5, and 9, explain how to determine whether a number is divisible by
Important: In questions 62 and 63, provide an explanation for each answer! Correct answer without explanation will not
receive full credit.
Examples of explanations: The number 4005 is not divisible by 6 because it is not divisible by 2. The number 4005 is divisible by 15 since it is
divisible by both 3 and 5.
62. Which of the following numbers divide the number 2,010?
6, 12, 15, 18
63. Which of the following numbers divide the number 1,245?
6, 12, 15, 18
64. Find prime factorizations of 2,010 and 1,245.
65. Find the greatest common factor and the least common multiple of 2,010 and 1,245.
66. The GCF of 66 and x is 11; the LCM of 66 and x is 858. Find x.
67. The GCF of two numbers m and n is 12, their LCM is 600, and both m and n are less than 500. Find m and n.
71. Real numbers A, B, C, D, E, and F are represented by points on the number line below.
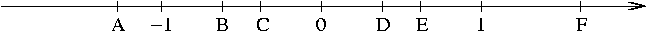
Determine the following if each answer is one of the numbers shown:
72. First read this chapter about real numbers.
Daniel writes 0.4<0.13 "because 4 is less than 13". Is he correct or wrong? Explain the correct reasoning
Recall: to solve an equation means to find all solutions, i.e. all numbers x that make the equality true.
Solve the following equations over the set of real numbers (i.e. find all real solutions of these equations). Show all steps of your solutions. Make sure that you can justify each step (recall that you can add the same number to both sides of an equation, subtract the same number from both sides of an equation, multiply both sides of an equation by the same number, or divide both sides of an equation by the same nonzero number. Be careful with division: if dividing by a variable/expression, remember that division is legal only when the variable/expression is nonzero!)
81. 2x+5=19
82. 2x+5=4x+11
83. 3x=5x
84. 3x+(x/2)=5-(x/3)
85. 3/x=9
86. x2=16
87. x3=-27
88. (x-3)(x+5)=0
89. x2+2x-35=0
90. 2x2+7x-4=0
91. 3x2-4x-5=0
92. 2x2-5x+7=0
93. (x+2)(x-5)=6
94. x(x-3)=(2x+1)(x+2)-8
101. In a small town, three children deliver all the newspapers. Abby delivers 3 times as many papers as Bob, and Connie delivers 13 more than Abby. If the three children deliver a total of 496 papers, how many papers does each deliver?
102. The formula for converting degrees Celcius (C) to degrees Fahrenheit (F) is F=(9/5)C+32. Your European friend asks you how warm it is now in Fresno. Your outdoor thermometer shows 80 degrees Fahrenheit. How many degrees Celcius is it?
103. Two silk butterflies and a silk rose cost $18. One silk butterfly and a silk rose cost $11. What is the cost of each?
104. A teacher instructed her class as follows: Take any number and add 15 to it. Now multiply that sum by 4. Next subtract 8 and divide the difference by 4. Now subtract 12 from the quotient and tell me the answer, I will tell you the original number. Analyze the instructions to see how the teacher was able to determine the original number.
105. Make up your own procedure similar to that in Problem 4. Test it by asking your group members to follow the steps you give them and tell you the result.
106. For an event at school, 812 tickets were sold for a total of $1912. If students paid $2 per ticket and nonstudents paid $3 per ticket, how many student tickets were sold?
111. One leg of a right triangle is 2 cm longer than the other leg, and the hypothenuse is 3 cm longer than the shorter leg. Find all sides of the triangle. (Hint: use Pythagorean Theorem.)
112. Estimate the number Pi as follows: consider a circle of radius 1. Its circumference is 2Pi.
Remark: similar procedure can be done with regular polygons with more than 6 sides. The more sides, the harder and longer calculations, but the better the estimate. As many groups indicated in their projects, Archimedes used polygons with up to 96 sides.
121. Find the height of a regular tetrahedron with edge 1 cm. Find its volume.
122. Find the volume of the ice cream cone pictured.
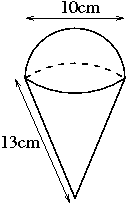
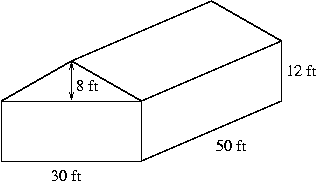
123. Find the volume of the house pictured.
124. Find the surface area of the ice cream cone pictured above.
125. Find the surface area of the house pictured above.
131. An equilateral triangle with sides 2008 units long is divided into smaller equilateral triangles with sides 4 units long. How many of these small triangles are there in the big one?
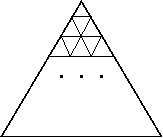
132. How many times longer is the perimeter of the big triangle than the perimeter of each small triangle in problem 131?
133. In problems 123 and 125, you found the volume and surface area of a house. (Correct answers are: Volume = 24000 ft3, Surface Area = 5360 ft2.) What are the volume and surface area of the house shown below?
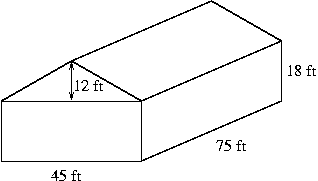
141. Suppose you are given an unfamiliar book. You have 10 minutes to estimate (not just guess!) how long it will take you to read this book. How can you do this? (Hint: use proportional reasoning!)
Solve each of the following problems in at least two different ways. At least one of your solutions should be very simple (accessible to a first-grader, i.e. should not use fractions or anything a first-grader will not understand).
142. Aby can run 5 laps in 12 minutes. Ben can run 6 laps in 14 minutes. Who is the faster runner?
143. Two camps of Scouts are having pizza parties. The Bunny Camp ordered enough so that every 5 campers will have 2 pizzas. The Fox Camp ordered enough so that every 7 campers will have 3 pizzas. If within each camp the pizzas are split equally, campers of which camp will eat more pizza?